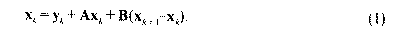
Közgazdasági Szemle, XLII. évf., 1995. 7-8. sz. (650-666. o.)

BRÓDY ANDRÁS

Bródy András az MTA Közgazdaságtudományi Intézetének tudományos tanácsadója.

Növekedés, csőd és ciklusok

(A végtelen modell csonkítása és spektruma)

A leírás a gazdaság már ismert dinamikus egyenletéből indult ki. Ezt szintén Leontief állította fel a következő formában (LEONTIEF [1953] 82-88. o.):

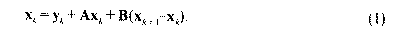
Itt az A mátrix a folyó ráfordítások együtthatóiból alkotott mátrix, B a tőkelekötések mátrixa, x pedig a teljes termelések vektora. A zárójelben tehát a termelés kívánt növekedése áll, s az egyenlet azt mondja ki, hogy a teljes termelésnek fedeznie kell a végső fogyasztást, a folyó ráfordításokat és a növekedéshez szükséges beruházásokat.

Tudjuk, hogy ha a gazdaság produktív, tehát a folyó ráfordítások kisebbek, mint a kibocsátás, akkor A legnagyobb sajátértéke kisebb 1­nél. Ekkor létezik és szigorúan pozitív Q = (1-A)^-1, az úgynevezett Leontief­inverz. Ha ezzel beszorozzuk az (1) egyenletet, akkor a következő összefüggést nyerjük:

Ha tehát adott az y végső fogyasztás és adott a kapacitások megkívánt növekedése, akkor kiszámítható az ehhez szükséges teljes termelés. Az persze külön vizsgálatot követel, hogy az adott évre már létrejöttek­e az ehhez szükséges kapacitások. Éppen ez a kérdés vezet a szomszédos évek vizsgálatához és az általánosabb ábrázoláshoz, amely biztosítani kívánja a megfelelő kapacitásokat is a figyelembe vett évek teljes sorára. Megemlítendő, hogy a (2) egyenletből kiszámítható az úgynevezett zárt rendszer egyensúlyi növekedési üteme és pályája is. Ekkor feltesszük azt, hogy y = 0, azaz nincsen külső vagyis "végső" fogyasztás.¹

Nem tudunk azonban válaszolni arra a kérdésre, hogyan befolyásolja az y_k értékek valamely adott (t=k, k+ 1,...) idősora az ehhez rendre szükséges évenként x teljes termeléseket. Minden új év egy új (1) alakú egyenletet hoz, de semelyiket sem lehet önmagában, a többitől függetlenül megoldani, mivel mindegyik egyenlet tartalmazza a soron következő év x teljes termelési szintjeit is. Nem tudjuk tehát biztosítani azt, hogy a számított értékek egy ellentmondásmentes, tehát megvalósítható termelési idősort adjanak.

Ezt a feladatot oldotta meg Leontief, amikor felírta az (elméletileg mindkét irányban végtelen) hipermátrixot,² amely összeköti az egymással szomszédos éveket:

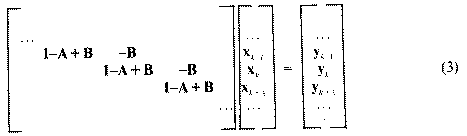
E mátrix inverzének, az úgynevezett dinamikus inverznek létezését és kiszámításának módját az irodalom behatóan tárgyalta. Leontief eredeti levezetése bemutatta azt a végtelen hatványsort, amely az inverz minden sorában (és oszlopában) megjelenik. Megemlítette azt is, hogy e hatványsor bizonyos esetekben divergálhat, és meghatározta azt a kritikus pontot, amikor a mátrix átlójában álló 1-A + B szingulárissá válik, és így lehetetlenné teszi az inverziót.

Az ilyen kétszeresen is végtelen mátrixnak a véges formáktól eltérő sajátságai is vannak. Erre mutat a következő két megfontolás. A végtelen hipermátrixnak végtelen hipersajátvektora a csupa egységmátrixból álló e=[..., 1, 1,..., 1,...]^T összegező vektor. Ha beszorozzuk a fenti mátrixszal, akkor kiejtve a minden sorban pozitív és negatív előjellel álló B mátrixokat, minden elemében csak az 1-A mátrixszal szorzódik. Az 1-A mátrix tehát a végtelen mátrix egyik hipersajátértéke, habár nem sajátértéke semmilyen véges szeletének. Ha tehát a végtelen hipermátrixnak van inverze, akkor ennek is sajátvektora marad a fenti összegező vektor. Ez a vektor az inverzben a hipersajátérték reciprokával, tehát a Q mátrixszal szorzódik. Ezért az inverz minden sorának (és minden oszlopának) összege Q.

Ez utóbbi sajátosságnak egyszerű gazdasági indoka van. A teljes ráfordítás mindig pontosan Q­szoros. A hipermátrix a szükséges ráfordításokat csupán elosztja a különböző évekre, teljes összegét nem változtatja meg. Ezt a matematikai sajátosságot már Leontief részletesebben bizonyította.

A végtelen hipermátrix azonban szinguláris, bár minden véges szelete reguláris. Hipersajátértékei között ugyanis szerepel a zérusmátrix. A (2) egyenletből kiszámítható a zárt rendszer egyensúlyi növekedésének rátája. Ennek értéke a QB mátrix legnagyobb és mindig pozitív sajátértékének a reciproka. Szorozzuk most be rendre a növekedése ütem, 1 + 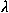, egymásra következő hatványaival a fenti végtelen összegező e hipervektor egyes egységmátrixait. Így olyan vektorhoz jutunk, amely ismét hipersajátvektor. De ez a vektor a beszorzás után minden sorban zérust ad eredményül, hiszen éppen ez a hosszú távú egyensúlyi megoldás feltétele, és ebből számítottuk ki 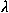értékét. A végtelen hipermátrix tehát szinguláris, mert van zérus sajátértéke.

A gyakorlati számítások, amelyek mindig a végtelen mátrix egy véges szeletére vonatkoztak, jól konvergáltak. PETRI [1972] azt is bebizonyította, hogy az időegység kis módosításával minden 1-A + B alakú mátrix esetleges szingularitása megszüntethető. E mátrix inverze azonban nem biztosan pozitív. A negatív elemek felbukkanása gazdaságilag értelmezhetetlen. Létezésük azt jelenti, hogy valamiképpen lehetséges ravaszul kevesebbet termelve mégis többet fogyasztani, vagy (megfordítva) kisebb fogyasztás esetleg csak nagyobb termelés árán biztosítható. Mindkét eset ellentmond a józan észnek és minden eddigi gazdasági tapasztalatunknak.

Az a feladatunk hát, hogy közelebbről szemügyre vegyük ezt a kérdést, és indokokat találjunk arra, ha mégis el kell fogadnunk ezt az ellentmondást. Ha pedig oka valamely sajátos körülmény, akkor javítanunk kell a számítás menetén, hogy ne álljon elő ilyen zavaró mozzanat.

A csonkításról

Mint matematikai problémát elméleti értelemben fel tudjuk fogni, meg tudjuk vizsgálni, sőt kezelni is tudjuk a végtelen mátrixokat. A számítógép azonban erre közvetlenül nem képes, mert memóriája véges. A tényleges számítás a végtelen mátrixnak mindig csak véges szeletét tudja a gépbe gyömöszölni. A sorok és oszlopok végtelen menetét meg kell csonkítani, mind a kezdetén (tehát a mátrix felső bal sarkában), mind a végső időpontban (a jobb alsó sarokban). Csak így faraghatunk ki invertálható négyzetes mátrixot. Az adatok tényleges hiánya is korlátozhatja a számítás terjedelmét. Bár az elméleti helytállóság megkívánná a végtelen jövőbe nyúló fogyasztási idősor megadását, mindig csak rövidebb, legfeljebb tíz­ vagy húszéves idősort tudunk összeállítani.

Sok függ tehát a csonkítás tényleges kivitelezésétől. Ha az átlóban álló ismétlődő 1-A + B mátrixot önmagában invertáljuk, akkor ennek gyakorta lehetnek negatív elemei. Ha most a jobb alsó sarkot is erre az alakra csonkítjuk:

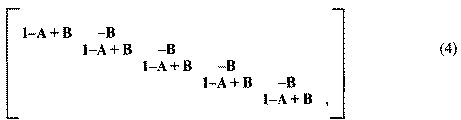
akkor elkerülhetetlenek a további bonyodalmak. Miért? A negatív előjelű B mátrixok, amelyek az átlóval párhuzamos következő diagonálisban állnak, a következő év szükséges ráfordításai. Másképpen nem volna elégséges kapacitás a szükséges tevékenységek elvégzésére. Ezekkel szemben állnak a pozitív előjelű B mátrixok a főátlóban. A pozitív előjel azt jelenti, hogy ezek az adott évek kibocsátásai. A kétszeres szerepeltetés elméletileg nem kifogásolható. Neumann János találta ki, hogy így lehet ábrázolni azt az állótőkét, amely megmarad a termelési folyamatban, több időszakaszra terjedő élettartama alatt. Sraffa és az úgynevezett Economic Activity Analysis művelői is kihasználták a matematikai tárgyalásnak ezt az elméleti lehetőségét a tőke korrekt ábrázolására.

Ez a matematikai leírás a tőkét sajátos ikerterméknek tekinti, amely csak abban különbözik az egyéb termékektől, hogy eredeti helyén maradva kerül vissza a termelési folyamatba. Ez esetben, mint egy­egy év termékét, össze szabad vonni az adott év folyó ráfordításaival, illetve kibocsátásaival.³ De ennek az alapjában szellemes és helyes ábrázolásmódnak következményei is vannak. Lehetetlenné teszi, hogy egy­egy évet a többitől elszigetelve kezeljünk. Figyelni kell arra, hogy ezeket a mesterséges "tőkefolyamokat", egymástól elszakíthatatlan ráfordítások és kibocsátások formájában együtt tartsuk. Mesterségesnek neveztük őket, mert a valóságban tőkeállagok és csak (elképzelt) év végi ki­ és ugyanakkor beáramlásuk teszi lehetővé a sajátos matematikai leírást, azt tehát, hogy ráfordításként is és kibocsátásként is megjelenjenek.

A (4) egyenlet az elméletileg végtelen mátrix csonkításakor levágja az utolsó évhez tartozó negatív előjelű B mátrixot. Ez a mátrix matematikailag már a következő, a számításban figyelembe nem vett évhez tartozik. Ezért úgy véljük, hogy lehasíthatjuk és figyelmen kívül hagyhatjuk. Mivel azonban itt ikertermékekről van szó, a mátrixnak mindig együtt kellene maradnia ikrével. Ekkor, mint láttuk, ellentétes előjelük révén általában kioltják egymás hatását, csupán átmeneti hatást hagyva hátra. A csonkítás miatt ez most lehetetlenné vált. Ezért van az, hogy az 1-A + B mátrix, mivel maga is ilyen csonkítás eredménye, szingulárissá válhat, vagy inverzének negatív elemei lehetnek, tehát általában szólva "kellemetlenül" viselkedik.

Az eredeti (1) egyenletben csupán egyetlen B mátrix szerepelt, amely a termelési szintek növekedésével szorzódik. Csak a (3) egyenlet helyettesítette ezt a növekedést két egymásra következő év teljes termelésével, amelyeket két (esetleg egymástól eltérő, mert időben is változó⁴) B mátrixszal kell megszorozni. A csonkítás folyamán azonban meggyilkoltuk a negatív előjelű ikertestvért, amit a megmaradó pozitív előjelű B drágán megtorol rajtunk. Elrontja (lefelé torzítja) a számított teljes termelési szinteket. Az utolsó évben ugyanis furcsán kirobbanó látszólagos kibocsátáshoz jutunk. Erre a rendszer, ha normálisan működik, semmi esetre sem képes. Ez a kibocsátás, Bx, nem kevesebb, és nem is más, mint a gazdaságba befektetett teljes tőke összege. Ezt nem tekinthetjük tiszta lelkiismerettel az utolsó év végső kibocsátásának. A szó szoros értelmében persze a rendszer valóban ezt adja át a következő éveknek, a gazdaság jövőjének. De ez átadás, és nem kibocsátás. Nem egészen így gondoltuk a dolgot. Még ha el is döntjük, hogy a következő évben abbahagyjuk a termelést (és általában felhagyunk minden gazdasági tevékenységgel), még akkor sem tudjuk eladni a piacon a gazdaság egész tőkéjét (és biztosan nem ebben az utolsó évben).

Összefoglalóan: ha így csonkítjuk a mátrixot, akkor egy olyan kérdésre kapunk választ, ami önmagában ugyan jogosult és értelmes, de semmiképpen sem azonos az eredetileg feltett kérdéssel. Eredeti kérdésünk az volt, hogy mi a teljes termelésnek az az idősora, amely éppen az előírt évi végső fogyasztásokat teszi lehetővé. Magától értetődőnek tekintettük, azért ki sem mondtuk, hogy a gazdaságnak működnie kell a számítás utolsó éve utáni időszakban is. Semmiképpen sem akartuk a gazdasági rendszert tönkretenni, nem akartuk csődbe kergetni vagy pusztulásig megcsapolni.

E helyett, a megadott csonkítással, a végső felszámolásba, teljes megszűnésbe kényszerített gazdaság termelésének idősorát számítjuk ki. Ez a kérdés és a rá kapott válasz egyáltalában nem olyan abszurd, mint azt az éles fogalmazás mutatja. Sőt: a kérdés elméletileg igen fontos és érdekes. Nálunk bizonyára nem nélkülöz némi morbid aktualitást sem. De biztosan nem ez volt az a kérdés, amire Leontief eredetileg válaszolni akart.

Negyven éven keresztül megterveztük a beruházásokat. De ha egyszer megtervezzük az új kapacitások létrehozását, akkor nyilván meg kell tervezni a régi, elhasznált vagy elavulttá lett kapacitások felszámolását is. Ez azonban nem történt meg.⁵ Ezért szakadt nyakunkba egyszerre a kilencvenes években a végsőkig halogatott, de a piacgazdaság körülményei közt tovább már nem halasztható feladat. Ezt a feladatot, mint az addigiakat is, politikailag és nem szakmailag kezelték, alighanem a kelleténél nagyobb veszteséget okozva. Ahogyan a beruházások gazdaságosságának meglehetősen bonyolult, de szakmailag elég jól és részletesen kidolgozott módszertana van, hasonlóan a gazdasági tevékenységek beszüntetésének is léteznek szabályai. Mindkettőt jócskán elhanyagolták nálunk a gazdaság mindenkori vezetői.

Itt mégis Leontief eredeti kérdésére keressük a választ. Hogyan módosítsuk tehát a csonkítás eljárását úgy, hogy a normális fejlődés menete és ne a csőd menetrendje adódjon a számításokból? Sokféle változat javasolható, hiszen a számítás befejezte utáni évekre különféle feltételeket szabhatunk. Kiköthetnénk például, hogy a gazdaság, miután kielégítette az előírt feltételeket, induljon tovább az egyensúlyi növekedés irányában. Vizsgálhatnánk azt is, hogy milyen speciális növekedési útvonal volna lehetséges és kívánatos a feladatok teljesítése után. Mindez azonban további feltevések modellezését, esetleg optimalizálását kívánná meg. Ez persze lehetséges, sőt éppen erre ad általános keretet a modell. Mégis itt bonyolítaná az alapvető probléma bemutatását, és valamilyen partikuláris megoldáshoz vezetne. Ezért a legegyszerűbb megoldást fogom bemutatni, mert ez teszi a tárgyalást, magyarázatot és a számpéldákat a legvilágosabbá.

Rendezzük be a számítás mátrixát a következőképpen:

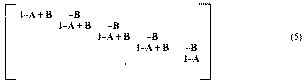
Egyetlen és látszólag apró változtatás, hogy a jobb alsó sarokban elhagytuk a pozitív előjelű B mátrixot. Mint a mátrixalgebrából tudjuk, ha az eredeti mátrix csökkent, akkor az inverze növekedni fog. S valóban az inverz jobb alsó sarkában az eddig esetleg negatív elemeket is tartalmazó mátrix helyett a mindig szigorúan pozitív Q mátrix fog állni. Tulajdonképpen, mint mindjárt számszerűen is bemutatjuk, csak ezzel tudunk eleget tenni a Leontief által elméletileg levezetett törvényszerűségnek, hogy az inverz minden sorának Q legyen az összege. Ezzel egyben elejét is vettük annak, hogy a fogyasztás valamilyen elemének csökkentése megnövelje a termelést. A dinamikus inverzzel való szorzás most már biztosan pozitív eredményt fog adni.

A tőkemátrix elhagyásával viszont nyilván elhanyagoltuk az utolsó évi beruházásokat, amelyek persze csak a következő években fogják kifejteni kapacitásbővítő hatásukat. Tehát a javasolt és bemutatott módosítás elvileg még mindig pontatlan és elégtelen. Az utolsó évre "egyszerű újratermelést" feltételezve, elhagytuk a további növekedéshez szükséges beruházásokat.

Mi legyen hát a további növekedés szükséges ráfordításaival? Javaslatom az, hogy vegyük őket figyelembe az utolsó év végső fogyasztásának megfelelő növelésével. Ez látszik a legegyszerűbb módszernek, hogy kikerüljünk a kátyúból. Nem kifogásolható elméletileg sem, mert ez a beruházás valóban végső, külső fogyasztás a számításmenet által felölelt évek szempontjából. Az új kapacitások, amiket ez a beruházás létrehoz, már csak a további, a számításban nem tárgyalt éveket szolgálja. A megoldás egyszerű, ráadásul csak kis változtatással jár. Mégis alapvetően megváltoztatja a számított adatokat és általános trendjüket, mint ezt a következő számpéldák mutatják.

Csőd és növekedés

Már egy ötéves láncolat megmutatja a két csonkítási eljárás sajátos eltérését. Összevont, csupán egyszektoros modellel számolunk. A számokat úgy választjuk meg hogy lehetőleg kerek számokat kapjunk. Ezért A = 0,8, tehát a működési többlet (operative surplus) húszszázalékos. Az inverz értéke tehát Q = 5, a végső fogyasztás ötszörösét kell megtermelni. Tegyük fel azt is, hogy a tőkeigényesség 1,8 évi termelésnek felel meg, azaz B = 1,8. A számok nem reálisak, mert így 11,1 százalékos az évi növekedés. A választást csupán a számításmenet áttekinthetősége indokolja.

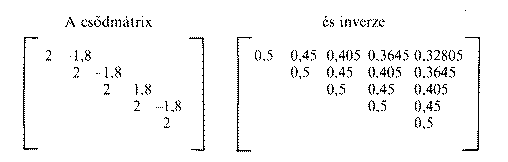
Az inverz főátlójában mindenütt az 1-A + B = 2 érték reciproka áll. A mátrix minden további eleme, akár az oszlop, akár a sor irányában haladunk tovább, elemenként mindig rendre 0,9­del szorzódik. Ez a B/(1-A+B), tehát az 1,8/2 értéknek felel meg, és a növekedési ütem reciproka. A normális növekedés inverze is hasonlóan alakul, csupán utolsó oszlopa eltérő. A növekedési mátrix jobb alsó sarkában 2 helyett 0,2 áll, ennek reciproka 5. Ez az előbbinek tízszerese, ezért az oszlop minden további eleme is az előbbi tízszerese.

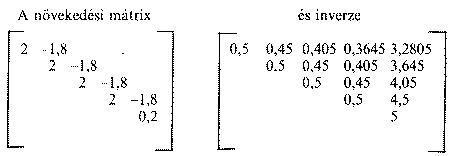
Látjuk tehát, hogy a javasolt módosítás csak az inverz utolsó oszlopát érinti, a két inverz minden egyéb tekintetben azonos. A módosítás nem változtatja meg még az utolsó oszlop arányait és számításmódját sem.⁶

A két inverz hasonlósága azt a látszatot kelti, hogy a csonkítás talán még egyszerűbben is megoldható. Ha csak az utolsó oszlop tér el, akkor mégis egyszerűbb volna a mondjuk a 2000. évig tartó elemzést 2001­ig kiszámítani, és aztán elhagyni az utolsó évét. Ez a megoldás azonban használhatatlan. Hasonlít ahhoz a tanácshoz, amely az utolsó vasúti kocsi rázkódását és lengését lekapcsolásával kívánja orvosolni. Akkor megint lesz egy utolsó kocsi, ami megint ráz, tehát azt is le kell kapcsolni, és így tovább, mindaddig, amíg a teljes szerelvény el nem fogyott. Az utolsó (és megváltoztatott) oszlop számértéke ugyanis már a számítás első évének eredményeit is módosítja.

Világosan mutatják ezt az inverzek sorösszegei, amelyek öt éven keresztül évente egységnyi végső fogyasztást biztosítanak. A teljes évi termelések értékei ekkor a következők:

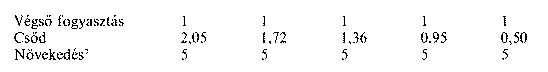
A csődhöz vezető megoldás tehát már az első évben lényegesen kisebb teljes termelést kíván. A különbséget nyilván a tőke felélése fedezi, s ezután is egyre rohamosabban fogy a rendszer termelése. A növekedés (itt csak egyszerű újratermelés) útvonalán pedig mindig ötszörös, tehát pontosan Q­szoros termelésre van szükség, mint ezt már Leontief bizonyította. Összeállíthatunk azonban valóban növekedő idősort is, amely exponenciálisan bővülő végső fogyasztást biztosít. A közel egyensúlyi évi tízszázalékos ütem a következő idősorokat adja:

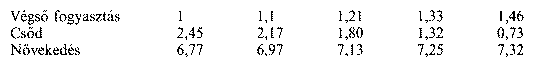
Egyértelmű, hogy a feladat reális megoldását csak az utolsó sor adatai adhatják meg. A csődmegoldás azonban igen érdekes elemzési szempontból, hiszen itt mindkét utolsó év teljes termelése már kisebb a végső fogyasztásnál is. A hatodik évre pedig a gazdaság szőröstül­bőröstül elfogyott, eltűnt. Ezek a csődöt jelző útvonalak kissé hasonlítanak a sokkterápiát szenvedett gazdaságok kezdeti nyomvonalaira. S nem árt itt arra sem figyelmeztetni, hogy minden túladóztatás és az ezzel járó túlelosztás előbb­utóbb elkerülhetetlenül ilyen tőkefelélő kényszerpályára hajt minden gazdaságot.

Forduljunk azonban a normális folyamatok felé! Mint a fentiekből is látható, semelyik megoldás sem elégítheti ki szabatosan a hosszú távú egyensúlyi növekedés feltételeit. Sőt a rendszer semmilyen véges szelete (és ennek inverze) sem illeszkedik, és nem is illeszkedhet az igazi egyensúlyhoz. Csak a végtelen és így, szigorúan tekintve, csak közvetve kezelhető modell engedi meg a teljes egyensúly elméletileg szabatos megoldását, kiszámítását, a pálya megindítását és követését. S még akkor is, ez csak elméletileg számított, tehát adathibákkal terhes, ezért csak közelítő és meglehetősen torzított képet adhat a valódi egyensúlyi fejlődésről.

Az igazi kérdés ilyen körülmények között inkább az, hogyan képes valamely adott és valóságos gazdasági rendszer egyáltalán az egyensúly közelében maradni, ha ezt az egyensúlyt sohasem tudjuk sem közvetlenül megfigyelni, sem megvalósítani, sem pedig pontosabban kiszámítani. Mégis azt tapasztaljuk, hogy a fejlett gazdaságok mindig csak néhány százalékkal térnek el közelítőleg kiszámítható és gyakran ki is számított egyensúlyi pályájuktól. Ha pedig egy rendetlen, válságos és kiegyensúlyozatlan gazdaságot vizsgálunk, még akkor sem nagyobb a mennyiségek relatív eltérése, mint húsz­harminc százalék, s ennél nagyobb eltávolodást csak egyes árak, bérek vagy fizetések esetében tapasztalhatunk, s akkor sem gyakran. S még mindezek a gazdaságilag már igen kártékonynak bizonyuló erőteljes eltérések is beleférnek a matematikai gondolkodás és elmélet számára az egyensúly közelében lefolyó kis perturbációk gondolatkörébe.

Ciklusok

Belátva a gazdaság bizonytalan voltát, ahol megvalósult harmóniát, a részek szabatos egyensúlyát hiába is keresnénk, vizsgáljuk meg, hogyan képes a gazdaság mégis megbirkózni az állandóan felmerülő kisebb­nagyobb eltérésekkel. A vizsgálat tárgya tehát most az, hogy ha az előbbiekben tárgyalt egyenletek a gyakorlatban nem teljesülnek, azaz egyenlőtlenségekké válnak, akkor az eltérések hogyan fogják meghatározni a rendszer tényleges pályáját. Kísérletet teszünk a gazdaság valóságos mozgásának felrajzolására, nem elégedve meg elméleti egyensúlyi állapotok egymásutánjával.

GOODWIN [1952] szellemes és egyszerű modellt alkotott az egyenlőtlenség hatására kialakuló gazdasági reakciók leírására. Gondolata a későbbiekben is rendkívül termékenynek bizonyult, és a gazdasági rendszerek lehetséges mozgásformáit vizsgáló matematikai elmélet egyik alappillére. A szabályozás hatásláncolatának kialakulását, mint ő is tette, az egyszerű újratermelés modelljén lehet a legvilágosabban bemutatni. Induljunk ki tehát a Leontief féle modell zárt és statikus változatából! Ez az önmagát minden évben eredeti formájában helyreállító gazdaság leírása. Egyenletei szimplák. A tőkeállag változatlan. Ezért csupán az éves folyó ráfordítások A mátrixára van szükség. A rendszer teljes egyensúlyát két, egymással duális kapcsolatban lévő egyenlet fogalmazza meg:

Itt p^T az egyensúlyi árak sorvektora. A képletek burkoltan kimondják az egyensúly fennállásának egy harmadik feltételét is: a növekedési ráta, 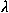értéke zérus. Ez a ráta csak akkor lehet zérus, ha az 1-A mátrix szinguláris. Másképpen kifejezve: A legnagyobb sajátértéke egységnyi. Az egyensúlyi árak és mennyiségek pedig A bal és jobb oldali sajátvektorai.

Mi történik most, ha a termelés, x, nem egyenlő az ehhez szükséges Ax felhasználással? És mi a következménye annak, ha az árak kisebbek vagy nagyobbak a költségeknél? Goodwin a klasszikusok ismert tételeihez fordul, Adam Smith megállapításait írja fel legegyszerűbb matematikai alakjukban: a túlkereslet áremelkedéshez vezet; a magas ár ösztönzi a termelést. Az ennek megfelelő két differenciálegyenlet (az idő szerinti deriválást a változó pontozásával jelezve):

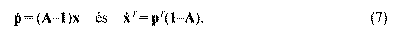
A két egyenletet összefűzve a másodfokú differenciálegyenlethez⁸ jutunk, akár az árak, akár a mennyiségek mozgását fejezzük ki. Vezessük be az 1-A = C jelölést hogy a végső mátrix szerkezete világosan kitűnjön. Kiindulva a termelés második deriváltjából,

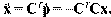
Írhatjuk tehát, hogy

Az önmaga transzponáltjával szorzott C mátrix úgynevezett Gram­féle szimmetrikus forma. Az ilyen mátrixnak minden sajátértéke valós. A mátrix ezenkívül szemidefinit, azaz csak zérus és pozitív sajátértékei lehetnek. Van vagy lehet tehát egy egyensúlyi x vektor, amely a zérus sajátértékhez tartozik, összes deriváltja zérus. Ez a vektor egy konstans értékű nyomvonalat ír le.

A (8) egyenletnek ezenkívül csupán különböző frekvenciákkal rezgő, tehát ciklikus megoldásai léteznek. Negatív számból vont négyzetgyök tisztán képzetes számhoz vezet. Az így nyert e^i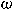t alakú megoldások (ahol 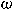² a fenti Gram­mátrix valamely pozitív sajátértéke) egy­egy lehetséges gazdasági ciklust írnak le. A ciklus hosszát a T=2/ 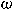képletből számítjuk.

Goodwin klasszikus logikával felállított egyenletrendszere jól magyarázza a ciklusok létrejöttének okát és elkerülhetetlenségét. Kevésbé meggyőző azonban a kapott számszerű eredmények tekintetében. A fenti Gram­féle mátrix valamennyi zérustól különböző sajátértéke ugyanis közel egységnyi, mert az A mátrix második és további sajátértékei igen kicsinyek. Ezért aztán a Gram­féle mátrix sajátértékeinek négyzetgyökei is közel lesznek 1­hez. A kapott ciklusok hossza így zömében 6 év körüli, s ez a hossz nem felel meg a tapasztalatoknak. Az irodalomból főként a készletek mozgásának 4-5 éves ciklusait, a 10-12 éves beruházási ciklusokat, a 20-25 éves hosszú vagy generációs ciklusokat és a 45-60 éves Kondratyev­hullámokat ismerjük. Ezeknek pedig egyike sem jelent meg Goodwin modelljében.

Egy húsz évvel későbbi dolgozatban (BRÓDY [1972]) ezért megkíséreltem Goodwin elmélete alapján a zárt dinamikus modell, tehát a C =1-A + 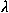B mátrix adta ciklushosszakat kiszámítani. A kapott frekvenciák már valamivel reálisabbnak mutatkoztak. A vizsgált hétszektoros modellt ezért illeszteni lehetett az Egyesült Államok 1958-1968. évi idősoraihoz is. Jelentkezett benne az ismert beruházási ciklus is, de a számított nyomvonal még mindig túl simának és "szépnek" bizonyult. Semmiképpen sem hasonlított a tényleges gazdasági rendszer tényleges adatainak képéhez. Túlságosan is egyszerű volt az elméleti pálya, hiányzott belőle a gazdaságstatisztikai adatsorok ismeretlen véletlen vagy kaotikus jellegű bizonytalansága, fluktuációja.

A végtelen dinamikus mátrix ismeretében most kísérletet lehet tenni a gazdasági ciklusok teljes spektrumának vizsgálatára. A gazdasági rendszert tehát végtelennek tekintjük, persze csak abban az értelemben, hogy nem korlátozzuk a gazdasági tevékenység időbeli lefolyását. Azaz nem végtelen számú terméket tételezünk fel, sőt ismét csak az egyetlen szektorra összevont gazdaságot tekintjük. Ebben a (talán túlzott) egyszerűsítésben arra a megfigyelésre támaszkodom, hogy egy nagy nem negatív mátrixnak csak sok kicsi és zérushoz közelálló sajátértéke van a legnagyobb és domináns sajátértéken kívül. Úgy látom, hogy ezeknek a kis, változó és csak pontatlanul megállapítható sajátértékeknek nincsen és elméletileg nem is lehet fontos szerepük a tapasztalható ciklusok kialakításában. Ez a sajátosság már az eredeti Goodwin­modell számszerű eredményeiből is kitűnik.

Most azonban az előbbinél megbízhatóbb és elfogadhatóbb számértékeket kell választanunk a modell felállításához. A profitrés (működési többlet, operatíve surplus, tehát a teljes gazdasági forgalom egységére jutó nyereség vagy tiszta jövedelem) a mai fejlett gazdaságokban átlagosan tíz százalék.⁹ Ez persze nem szilárd arány, mert körülbelül plusz­mínusz harminc százalékos relatív ingadozást tapasztalható a szélső 0,7 és 0,13 értékek közt. Az átlaggal fogunk számolni, hiszen itt elsősorban csak a nagyságrendek megállapítása a célunk és az, hogy a ciklusok lehetséges eloszlására vonatkozó támpontokat kapjunk.

A kiinduló adatok szokásos eltérésének és bizonytalanságának hatását majd a számítás elvégzése után vesszük figyelembe. Az összevont folyó ráfordítási mátrixot tehát az ennek megfelelő skalárral vesszük számításba. Ezért A = 0,9 és C = 1-A = 0,1 értékű. A tőkeigényesség, B, tehát a tőke/termelés hányados mintegy háromévi jövedelem lekötését jelzi, azaz B = 3. Ennek relatív ingadozása is hasonló az előbbi értékhez. E két érték 3,3 százalékos egyensúlyi növekedési rátát eredményez, és ez elég közeli a korunkban tapasztalt tényleges hosszú távú, szekuláris növekedési rátákhoz. A kiinduló adatok nagyságrendjei ezért legjobb tudomásom szerint reálisaknak tekinthetők.¹⁰

Ha felírjuk a kétszeresen végtelen Leontief­mátrixot, akkor ezeknek az adatoknak az alapján a (4) egyenletnek megfelelően az alábbi mátrix adódik:

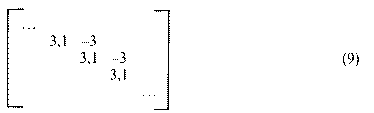
A mátrixnak csak kétfajta eleme van. A főátló minden eleme változatlanul C + B = 3,1, s a következő diagonálisban mindig -B = -3 áll. Ha a mátrixot saját transzponáltjával megszorozzuk, hogy eljussunk a megfelelő Gram­féle mátrixhoz, akkor is csak két elemet kell meghatározni. Minden főátlóban álló elem 2(B² + CB) + C² = 18,61. Mellette mind az alsó, mind a felső diagonálisban egyaránt -(B² + CB) = -9,3 áll. A keresett Gram­féle mátrix értékei ezért az alábbiak lesznek:

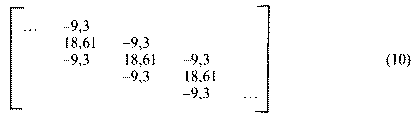
A mátrix legkisebb sajátértékét megbecsülhetjük az összegező [...1, 1,..., 1,...] vektorral szorozva. Ez minden esetben a 0,01 értékhez vezet, ami a 0,1 frekvenciát, tehát 2/ 0,1 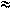63 év körüli ciklushosszat ad. Hasonlít a Kondratyev által felfedezett ciklushoz. Sajátos tulajdonsága van. Eddig úgy véltük, hogy csak az egyensúlyi vektor elemei lehetnek mind pozitívak. Most azt látjuk, hogy egy ciklikus mozgást kiváltó vektor is állhat csupa pozitív elemből. Ez azt jelenti, hogy itt olyan ciklussal van dolgunk, amely egyöntetűen, minden elemében szimultán módon (tehát fáziseltolódás nélkül) folyik le. A többi ciklus nem ilyen és nem is lehet ilyen, mert a hozzá tartozó sajátvektor változó előjelű.

Ha most ilyen változó előjelű egységekből álló vektorral szorzunk, akkor az elérhető legnagyobb sajátérték (az elemek abszolút értékének összege) 37,21. Ennek négyzetgyöke, 6,1, a frekvencia. Az ebből eredő ciklus hossza 2/ 6,1, ami csak kevéssel haladja meg az egy évet. De biztosan vannak még más frekvenciák is. A lehetséges ciklusok pontosabb és részletesebb leírásához csak úgy juthatunk, ha megtaláljuk a mátrix szabatos spektrális felbontását.

Szerencsékre olyan mátrixszal van dolgunk, amelyet a matematika már sokkal a számítógépek megjelenése előtt nemcsak részletesen tárgyalt, de numerikusan is elemzett. Ez a sajátos alakú mátrix a geodéziai munkában merült fel. Nem más, mint a háromszögelési mérések kiértékelésének alapját adó lánc (chain) mátrix. Ez, mint látjuk, tridiagonális mátrix, inverzét és sajátértékeit tetszőlegesen hosszú lánc esetében rég táblázatokba foglalták.¹¹ BODEWIG [1959] (421. o.) pontos képletet közöl az általános láncmátrix sajátértékeire is. Legyen a G_n Gram­féle mátrix olyan lánc, amelynek n tagja van, főátlójának minden eleme 2, mellékdiagonálisaiban pedig -1 áll. Akkor e mátrix n darab egymástól szigorúan különböző sajátértéke Bodewig alapján:

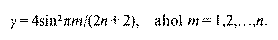
A lehetséges frekvenciák értéke ebből gyökvonással megállapítható. A frekvenciák spektruma 2sin(0) = 0 és 2sin(/2) = 2 intervallumban van. Ha a mátrix által ábrázolt évek száma, n, minden határon túl növekszik, akkor a legkisebb frekvencia zérushoz tart, míg a legnagyobbak láthatóan 2 alatt sűrűsödnek, s azt határértékben el is érik. A fentebbiekben számszerűen felállított és kiszámított lánc pedig a 9,3 G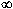, + 0,01 E mátrix, ahol most E jelöli az, egységmátrixot.

Mindennek következtében a csonkítatlan és végtelen dinamikus Leontief­rendszerből képzett tridiagonális Gram­mátrix, tehát a végtelen gazdasági rendszer mátrixának 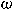frekvenciái (az egyensúlyi zérus értéken kívül) a már egyszerűbb megfontolások révén is kimondott

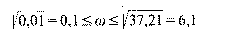
intervallumban találhatók. A gazdasági ciklusok hossza ezek szerint nyersen 1 és 63 év közt adódhat, mégpedig (s ennyivel tudunk most többet Bodewig képlete alapján) rendkívül sok (tulajdonképpen "végtelen számú"), 1 év körüli, de egymástól szigorúan eltérő hosszal bíró ciklust fogunk találni. Mint látni fogjuk, ebből adódik a gazdaságstatisztikai nyomvonalak sajátos, látszólag előrejelezhetetlen fluktuációja, "fűrészfogazottsága".

Bízhatunk­e a kiszámított nagyságok rendjében? Mivel a frekvenciát a C és a 2B + C mátrixok értékei határolják be, ezért a ciklushosszak lehetséges változása sem nagyobb a számítások elején tárgyalt lehetséges eltéréseknél. Tehát a hosszú ciklus lehet mintegy 20 évvel rövidebb is (kevésbé valószínű, hogy hosszabbnak adódjon), és biztosan csak egy van belőle. A rövid ciklusok lehetnek akár 10 hónaposak vagy másfél évesek is, de biztosan rendkívül sok közel egyforma van belőlük. S e két szélsőség közt található a szakirodalomban tárgyalt ciklusok egész választéka. Meglepetésünkre itt is mindenütt sok, egymástól csak kevéssé eltérő hosszal bíró ciklus bukkan fel.¹² Ezért oly nehéz hát a tetőzés és a válság mély fordulópontjainak szabatos megállapítása és előrejelzése.

Rövidebb ciklus a fenti modell alapján nem adódik. Vizsgáljuk meg újra, nem adódhat­e hosszabb ciklus. Már említettük az egyensúlyi növekedés vektorához tartozó zérus sajátértéket és frekvenciát. Ez a zérus érték végtelen ciklushossznak felel meg, és csak a végtelen láncmátrixban fordulhat elő, mint arra Bodewig képlete alapján következtethetünk.

A növekedésnek a (9) mátrixból felírható 3,1-3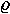 = 0 egyenlete szerint a növekedési ütem 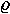= 1 + 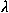= 3,1/3 =1,033. Ehhez hasonlóan azonban a (10) mátrix alapján már a másodfokú

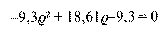
egyenletet fogalmazhatjuk meg. E másodfokú egyenletnek két megoldása van, és az ezeknek megfelelő két növekedési ütem végtelen hatványsorának vektorával beszorozva a mátrixot, mindkét esetben zérus lesz a kapott eredmény, tehát a sajátérték. A fenti egyenletnek azonban nemcsak az előbbi 1,033, hanem 0,976 is megoldása. Tehát nemcsak a 3,33 százalékos növekedés, hanem az ugyanilyen ráta szerinti csökkenés is megoldás. Márpedig csökkenő termelés nem oldja meg a gazdasági növekedés (1) egyenletét, amelyből kiindultunk. Látszólag ellentmondásra bukkantunk, mert a piaci mozgás nemcsak egyensúlyi növekedést, hanem (ugyanazon adatokból kiindulva) hasonló rátájú és szintén egyensúlyi csökkenést is lehetővé tesz. Mi a nyitja e furcsa új megoldásnak, amely - kimondatlanul - ott lappang már Smith és Ricardo téziseiben?

Ha a termelés egyensúlyi és egyensúlyi ütemben is növekszik, akkor az ár nem változik, hiszen minden piac egyensúlyban van. Ha az ár is eleve egyensúlyban volt, akkor a termelés valóban tovább növekedhet a régi ütemben. Az ehhez szükséges beruházásokra a kialakult profitrára szerinti nyereség kellő fedezetet nyújt. Ez a klasszikus teljes egyensúly ismert és elfogadott képe. A leírás azonban burkoltan tartalmaz egy ettől eltérő lehetőséget is.

Tegyük fel, hogy a termelés arányai egyensúlyban vannak, de nem növekednek, hanem éppenséggel csökkennek. Akkor egyenletes túlkínálat alakul ki minden piacon, s emiatt az árak csökkenni fognak, elvileg anélkül, hogy egyébként arányaikból kimozdulnának. S éppen ez az árcsökkenés lehet az oka a termelés általános csökkenésének, mivel az eladott termelés befolyó, de csökkent ellenértékéből már nem lehet a termelést a régi szinten folytatni. S ebben az esetben ez az önmagában zárt és logikus jelenségkomplexum éppen úgy képes önmaga megörökítésére, mint az egyensúlyi ütemben történő növekedés.

Az ilyenfajta jelenség az egyszerű újratermelés esetében nem következhet be, pontosabban szólva, az mindig stagnál, minthogy növekedési rátája zérus. Ezért e ráta negatívja is zérus, és nem is beszélhetünk a negatív ütemre való átváltás lehetőségéről. A növekedés körülményei közt azonban az ilyen hibás kör elméletileg létrejöhet, s mint tudjuk, ami elromolhat, az időnként el is szokott romlani.

S most egy logikailag talán túlságosan is merész, mert egyelőre nem teljesen alátámasztott következtetés adódik. Ha a termelés egyensúlyi változása lehet plusz vagy mínusz háromszázalékos, miközben az árak vagy változatlanok, vagy három százalékkal csökkennek, akkor talán kialakulhat egy mintegy 0,03 X 0,03 = 0,0009 frekvencianégyzetű ciklus is. A frekvencia ekkor 0,03, és ez a 2/ 0,3 képlet alapján mintegy kétszáz év tartamú ciklushoz vezet. Inkább a lehetőséget és nem a bizonyosságot fogalmaznám meg: a 200 éves gazdasági ciklus létezését nem tudom növekedés­ és cikluselméleti megfontolások alapján kizárni. Ezt látszik alátámasztani a fentiek alapján megszerkesztett és az alábbiakban bemutatott szimuláció is.

Illusztráció és diszkusszió

Mint említettük, a számítógép csak véges mátrixszokkal tud dolgozni, bár mostanára elég nagyokkal. Kiszámítottam egy 100 X 100­as Gram­féle láncmátrix összes sajátértékét. A mátrix a fenti (10) mátrix adatai alapján készült, de - véges lévén - az (5) előírás alapján csonkítottam, tehát jobb alsó sarkában nem a 18,61 érték, hanem csak 9,01 szerepel [mivel a (9) mátrix alsó sarkában nem 3,1, hanem a csonkítás miatt csak 0,1 áll]. A kapott ciklushosszak táblázata, években kifejezve:

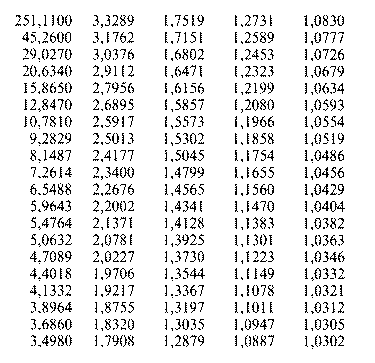
Szerepel benne egy 251 éves ciklus és egy Kondratyev­szerű hullám, amelynek hossza itt (a csonkítás következtében) csak 45 éves.¹³ Van négy kissé eltérő, de 4 évre kerekíthető és háromfajta 5 évre kerekíthető ciklushossz. Ötven különböző rövid ciklus hossza pedig 1,5 év alatt marad. A spektrum mindenesetre igen sajátos alakú, rendkívül furcsa tulajdonságokkal bíró trajektóriát hoz létre.

Nem tudjuk persze, hogy egy adott kezdeti állapot milyen erővel pendíti meg a lehetséges frekvenciák szerinti rezgéseket. Ezért a szimuláció egyforma és egységnyi koefficiensekkel számolt, a következő képlet alapján:

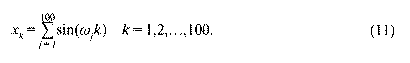
Mint látjuk, szigorúan periodikus függvénnyel van dolgunk, amelynek ezért nincs trendje, azaz stacionárius. Csakhogy a ciklusok hossza nem feltétlen racionális szám, ezért az ismétlődés legkisebb közös többszörösét nem tudtam kiszámítani. Ha azonban csak közelítő ismétlődést írunk elő, mondjuk 2 tizedes pontossággal (hogy a szabad szemmel látható kép közel azonosan térjen vissza), akkor is a fenti ciklushosszak alapján 10²³¹ évig kell várni, hogy az alábbi trajektória megismétlődhessen. A világ kezdete, az ősrobbanás óta azonban még csak 10⁶³ év telt el. Ennek következtében meglehetősen egyéni lefutást várhatunk, s valóban azt is kapunk.

Az első száz év alakulását az 1. ábra mutatja.

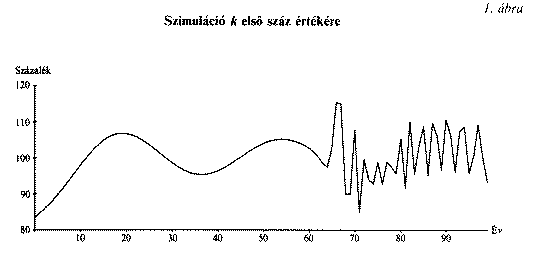
A szimultán, fáziskésés nélküli indítás és a sok egy év körüli periódushossz egyetlen sima és 40 évnél valamivel rövidebb ciklust hoz létre az első "félévszázadban". A hatvanadik éven túljutva, a trajektória jellege hirtelen megtörik, és kaotikusnak tűnő ingadozás lép fel. Az ingadozásban sok a hároméves ciklus (ez ismert jelenség a káosz matematikai irodalmában). A mozgás mégsem kaotikus, mert lineáris differenciálegyenletből származó egyszerű ciklusok kompozíciója. Csupán az okozza a káosz látszatát, hogy igen sok ciklus keveredik, ráadásul e ciklusok többsége közel egyéves időtartamú. A kaotikus viselkedés a rövid hullámok folyton változó interferenciájából ered. Sztochasztikus folyamatnak sem tekinthető, bár arra is hasonlít. A folyamat szigorúan determinisztikus. Megjegyzendő azonban, hogy az ismert valószínűségi eloszlásokat is szigorúan determinisztikus módon írja le a valószínűségszámítás, sőt a számítógép is szigorúan determinisztikus módon hozza létre a véletlen számokat, ha ezt írjuk elő számára.

Nincs tehát igazán segítségünkre ez a tudás. Még ha tudjuk is a 100 évet felölelő trajektóriáról, hogy az a látszat ellenére egyszerű szinuszhullámok egyvelege, akkor is legalább 300 év megbízható adatára volna szükség ahhoz, hogy következtetni tudjunk a 100 frekvencia, 100 fáziskésés és 100 amplitúdó nagyságára. Azt pedig, hogy 100 vagy 101, esetleg csak 99 frekvencia (vagy éppenséggel 2000 vagy még több) ismeretlen ciklus szerepel­e a valóságos gazdaság valóságos adatsorában, azt nem tudhatjuk és még nagyságrendileg is lehetetlen megbecsülni. Csupán a spektrum eloszlásának formájára ad felvilágosítást Bodewig idézett képlete.

Mindezért némi önkritikával tartozom a Szemle olvasóinak, akiknek három évvel ezelőtt (BRÓDY [1992]) bemutattam előrejelzésemet, amely a magyar gazdaság történeti idősorának cikluselemzésén alapult. A jövendölés eddig bevált, talán csak a várt fellendülés indult meg néhány hónappal korábban és bizonyul most erőtlenebbnek a reméltnél. Ezt most mégis hajlamos vagyok némi hályogkovácsi szerencsének is betudni.

Nem a ciklusok létezésében kezdtem kételkedni, mégcsak nem is abban, hogy gondos statisztikai munkával ne lehetne elválasztani a nagyobb erővel jelentkező ciklusokat az elhanyagolhatóaktól. Mégis, szembesülve a lehetséges ciklusok rendkívül nagy számával, csökkent a bizalmam a tekintetben, hogy a ciklus fordulópontjait a ma ismeretes eljárásokkal pontosan meghatározhassuk. Egy adott ciklus amplitudójának és fázisának meghatározása nem boszorkányság. Ha azonban felmerül a gyanú, hogy több, egymáshoz nagyon hasonló, de időtartama és ereje tekintetében mégis kissé eltérő ciklus együttes hatását kell felmérni, akkor a ma használatos módszereket alaposan újra kell gondolni.

A szemléltető, mintegy képi tájékoztatás érdekében kiszámítottam (szimuláltam) a fenti idősor későbbi menetére, mégpedig a k = 1900-2000 "évekre" kumulált GDP értékeit is. (Itt tehát az egyes évekre kapott és zérus várható értékű idősort évi növekedési rátának tekintettem - lásd a 2. ábrát).

Mégis, mintha az első világháború, a harmincas évek válsága, a második világháborúba vezető fellendülés, a hatvanas évek viszonylag ciklusmentes növekedése, de még a nyolcvanas évek recessziója is belelátható volna a grafikonba. Ez teljesen véletlen, hiszen a görbe menete semmilyen tényleges gazdaság képét nem tükrözi. Csupán az átlagos gazdaságok erre az időszakra megállapítható két reális makroadata, a megtakarítási ráta és a tőkeigényesség kelti mindazt a változatos rezgést, beleértve a hosszabb ciklusokat eltakaró sok kis ingadozást, amit az 2. ábrán láthatunk.

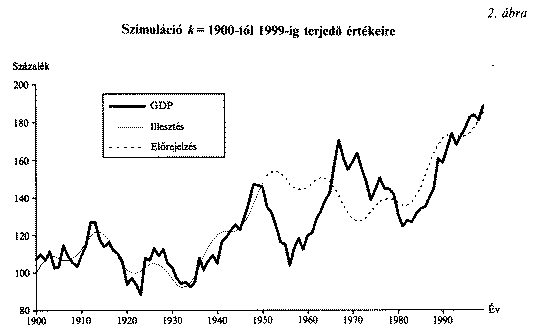
Megkíséreltem e mesterséges adatokhoz egy trendből, valamint 4, 12 és 42 éves ciklusokból álló idősort illeszteni az első ötven évre. Ez szorosan simul és elfogadhatóan leírja az adatok menetét. Aztán megkíséreltem ennek alapján "előrejelezni" a második ötven évet. Itt az első tíz évben roppant nagy az eltérés. Bár jelzi az 1956­ra bekövetkező visszaesést, de mértékét alábecsüli. Hasonlóan alábecsüli az erre következő fellendülést is. Végezetül azonban (óh, csodák csodája) 1980­tól az "ezredvégig" megint szépen illeszkedik a tényleges, azaz mesterségesen megszerkesztett adatokhoz.

A tanulság tehát egyelőre csak annyi, hogy a 100 ciklusból vett kis mintával mégis a vártnál jobban meg lehet közelíteni egy adott gazdasági rendszer nyomvonalát. Már három ciklus is viszonylag szorosan leírja a bonyolult menetet, s az illeszkedést megjavítani is lehetne a közelítő ciklusok hosszának optimális megválasztásával. A pontos és megbízható leírás és előrejelzés módszertana azonban mégis matematikai felülvizsgálatra szorul. E felülvizsgálat lényege az, hogy nem néhány (csekély számú) "legfontosabb" ciklus megállapítására kell törekedni, hanem a csak eloszlásában ismert, de ismeretlen számú ciklus által létrehozott nyomvonalat kell a lehető legegyszerűbb eszközökkel megközelíteni.

Ami pompásan sikerült, az a trend megközelítése volt. Ebben csak az a hiba, hogy - mint már említettem - az adatsor stacionárius, tehát nincs és nem is lehet trendje. Ha átmenetileg létrejön ennek látszata (a 251 éves ciklus éppen felfelé menő ágában), akkor ennek 125 időegység múlva megjön a böjtje. Esetünkben a nyolcadik 251 éves szinuszhullám éppen k = 2004­ben indul. Tehát előtte és utána 63-63 évig növekedőben van... Ennek pontosan eleget tesz a GDP ábrázolt menete, amely láthatóan a harmincas évek táján kezd fellendülni. Az addigi trend ugyanis csökkenést mutat.

Ennek tanulságát a fentinél határozatlanabbul tudom csak levonni. Talán gyümölcsöző lehet, ha a gazdasági trendet is valamiféle hosszú ciklusnak fogjuk fel. Ez ellen szól, hogy akkor az előrejelzés függ e ciklus feltételezett hosszától. Mint láttuk, éppen ez az az érték, amit elméletileg és gyakorlatilag egyaránt a legnehezebb megállapítani. Mindenképpen helyes volna azonban elgondolkodni azon, hogy a hagyományos felfogás, amely trendre, ciklusra és véletlen hatásra bontja a gazdasági idősorok elemzését, nem szorul­e némi módosításra a hatékonyabb előrejelzések érdekében. A "véletlent" a sok rövid periódus megmagyarázza. Itt módosítást csak a valószínűségi változó eloszlására vonatkozó feltételezések jelenthetnek, amelyeket a sajátértékek eloszlásából kell levezetni. A trendnek egy nagyon hosszú ciklussal való helyettesítése (e hossz haladja meg a vizsgált időszak mintegy húszszorosát) szintén nem jelenthet lényeges változást numerikus szempontból. De talán éppen a mozgás magyarázatának egyöntetűsége adhat némi új kapaszkodót azzal, hogy a gazdasági növekedést kvázistacionárius folyamatnak tekinti, a megfelelő megszorításokkal.

Az elemzés és előrejelzés matematikai módszereinek további javítására vonatkozó javaslat, a javaslatok természetének megfelelően, puhatolózó és bizonytalan. Határozottan ki kell mondani azonban egy, a kutatásból adódó, fontosnak és központinak tartott elméleti következtetést.

Mindeddig szinte kibékíthetetlen ellentétet, szöges ellentmondást véltünk vagy konstruáltunk a gazdaság viselkedésére vonatkozó ismert elméletek közt. Smith és Ricardo sima növekedést látott ott, ahol Sismondi és Marx a válságokat hangsúlyozta, Slutzky és az ökonometria pedig a véletlen megrázkódtatások hatására kialakuló sztochasztikus és kaotikus jelenségeket. Ez az alapvető látásmód vagy szemlélet határozta meg aztán mindhárom iskola fogalmait, terminológiáját, tudományos és vitamódszereit, valamint gyakorlati javaslatait is.

A három jellegzetesen eltérő felfogás az idők folyamán szinte misztikus ideológiai hadrendekké, politikai pártok és programok kristályosodási pontjává merevült. A liberalizmus védszentje Smith, a szocializmusé Marx, míg a szakszerűség az adatok és a matematika racionalitása mögé sáncolja magát. Itt azonban bebizonyosult, hogy a valóság mindhárom arca egyazon egyszerű összefüggésrendszer működésének eredménye. A fenti modellnek mind a három mozgásforma a sajátja, mindhármat jól leírja és ábrázolja. Logikailag ellentmondásmentes és egyöntetű felfogásra épül, s ez a felfogás egyik iskola alapvető szemléletével és téziseivel sincs ellentétben. Ráadásul a modell elemi eszközökkel dolgozik és egy igen szimpla lineáris differenciálegyenletre épül.

A modellben, mint a gazdasági valóságban is, a háromfajta lehetséges mozgás eredeti természetes egységében és összefüggésében nyilvánul meg. Az egyes mozgásformáknak megfelelő három szemlélet ezért valójában nem is lehet ellentétes, hiszen csupán a valóság három különböző, de együttesen létező és egyformán lényeges vonását ragadja meg.

E következtetés kimondását és félreérthetetlen megfogalmazását látom a kutatás, sőt egész eddigi munkám legfőbb eredményének.

Hivatkozások

BODEWIG, E. [1959]: Matrix Calculus. North Holland, Amszterdam.

BRÓDY ANDRÁS [1972]: An Input-Output model for the market. Megjelent: A. Bródy and A. P. Carter (szerk.): Input­Output Techniques. North Holland, Amszterdam.

BRÓDY ANDRÁS [1992]: Gazdaságunk az ezredfordulón. Közgazdasági Szemle, 9. sz.

GOODWIN, R.: [1952]: Static and dynamic linear equilibrium models. Megjelent: Proceedings of the First International Input­Output Conference. Driebergen, Hollandia.

LEONTIEF, W. [1953]: Studies in the structure of the American economy. Oxford University Press, Oxford.

LEONTIEF, W. [1970]: The dynamic inverse. Megjelent: A. P. Carter and A. Bródy (szerk.): Contributions to Input­Output Analysis. North Holland, Amszterdam.

PETRI, P. [1972]: Convergence and temporal structure in the Leontief dynamic model. Megjelent: A. Bródy and A. P. Carter (szerk.): Input­Output Techniques. North Holland, Amszterdam.

¹ Pontosabban szólva ilyenkor ez a végső fogyasztás is a rendszer belső felhasználása. Kibővítjük az A mátrixot a végső felhasználók (általában a háztartások, állam, külkereskedelem stb.) szektoraival.

² Hipermátrixnak nevezzük az olyan mátrixot, amelynek elemei maguk is mátrixok. Hasonlóan definiálhatjuk a hipermátrix hipersajátvektorát is. Ez tehát egy mátrixokból álló vektor lesz. A hipersajátérték ilyenkor nem skaláris mennyiség, hanem maga is mátrix, és a sajátérték reciprokát a mátrix invertálásával számíthatjuk ki.

³ Ezzel megoldható az úgynevezett dimenziós ellentét. E szerint tőkét (stock) és áramlatot (flow) nem szabad közvetlenül összegezni, mert nem azonos a mértékegységük.

⁴ Leontief eredeti modellje a technikai változását is leírhatóvá teszi, mert változó elemű mátrixokat használ. A felmerülő problémákat azonban könnyebb így elemezni és magyarázni. A javasolt megoldás változó mátrixok esetén is alkalmazható.

⁵ A tervezést szakszerűbben felhasználó országokban, például Japánban, a feleslegessé vált vállalatok és ágazatok békés és gazdaságos halála, euthanáziája szintén tárgya a tervezésnek. A gazdaság technikai elmaradása tehát nem a tervezés szükségszerű következménye. Az elmaradásért éppen a figyelmetlen és szakszerűtlen tervezést és az ebből eredő hibás érdekeltségi rendszert okolhatjuk.

⁶ Az említett angol nyelvű változat függelékében részletesen bizonyítottam, hogy ez a törvényszerűség általános, tehát a sokszektoros modellek esetében is fennáll.

⁷ Itt ez természetesen nem valódi növekedés, hanem stagnálás, egyszerű újratermelés, mert a végső fogyasztás sem növekszik.

⁸ A fenti egyenletek, mint Goodwin későbbi híresebb modelljei is, úgynevezett hamiltoni formaként írhatok le. Ez lényegesen segíti a matematikai elmélet kialakítását és egységesítését. Mivel a hamiltoniánusok elmélete fizikai megfontolásokon alapult, külön és részletes ismertetését tervezem. Itt csak a mátrixelméletből is levezethető sajátosságokra támaszkodom.

⁹ Ne feledjük, hogy ugyanez a többlet a nemzeti jövedelem vagy a GDP értékéhez viszonyítva sokkal nagyobb, a duplája vagy még magasabbnak adódik. A fenti adatok tehát mintegy 10 és 30 százalék közötti megtakarítási rátákat fognak át, ha a jövedelmekhez viszonyítjuk őket. Ha pedig teljes termelésnek a tervgazdaságokban megismert igen alacsony jövedelemtermelési hányadát vesszük figyelembe, az arány még a 40 százalékot is jócskán meghaladhatja.

¹⁰ Ezek a nagyságrendek viszonylagosan változatlanok az ismert történelem és igen eltérő társadalmi formációk esetében, függetlenül attól, hogy a megtakarítások fűkunyhókban vagy felhőkarcolókban, ásókban vagy exkavátorokban testesülnek­e meg. Nincs és nem volt társadalom, amely munkájának felét megtakarította, vagy egészét felélte volna. A tartós eszközök mindig és mindenütt legalább 1 évi munkába kerültek, és soha és sehol nem érték el 7 év munkáját. A nagyságrendeket valószínűleg az életidő szokásos hosszától függő szemléletünk alakítja. Ez szabja meg, hogy mi "rövid" és mi "hosszú" időtartam a gazdaságban. A gazdasági folyamatoknak az év (nem a másodperc és nem az ezer év) a "természetes" mértékegysége.

¹¹ Ezek a láncok alkotják a kijelölt geodéziai hálózatoknak azt a részét, amit már a bonyodalmas helyi mérések elvégzése és matematikai kiegyenlítése előtt, mintegy az irodában ülve, előre invertálni lehet.

¹² A következő fejezet felsorolja egy speciálisan összeállított, tehát csonkított 100 X 100­as mátrix valamennyi ciklushosszát.

¹³ A csonkítás csak a legkisebb sajátértékeket csökkenti észrevehetően, és a nagyobb sajátértékeket csak elenyésző mértékben módosítja. A bizonytalanság éppen a két leghosszabb ciklus tekintetében a legnagyobb. A leghosszabb és mintegy 200 évesnek vélt ciklus roppant bizonytalan. Létezését a modell ugyan alátámasztja, mert valamilyen hosszú ciklusnak léteznie kell, hogy mind a 100 sajátértékről el tudjunk számolni. A csonkítás formája azonban nem egyértelmű. Ha például a jobb alsó sarokban álló 1-A = 0,1 értékhez hozzáadjuk , értékét, az így adódó 0,133 érték körülbelül 200 éves hosszat eredményez.